Cómo segmentar una imagen para un reconocimiento de caracteres OCR con R

En una entrada anterior nos planteábamos cómo reconocer caracteres de una imagen con tesseract. En esta entrada describimos un método para encontrar las cajas relevantes que contienen información en la imagen. Empleamos un paquete que he desarrollado y que, entre otras características, clasifica las regiones de una imagen según si tienen el mismo color y si los puntos están conectados o no.

Primero instalamos el paquete matchmatrix, especializado en matrices, descargándolo de internet, así como el paquete png para leer ficheros png.

install.packages("https://torres.epv.uniovi.es/centon/graphics/matchmatrix_0.0.1.tar.gz", repos = NULL, type = "source")
library(png) # Para leer y escribir PNG
library(matchmatrix)  # Para trabajar con matrices de PNG

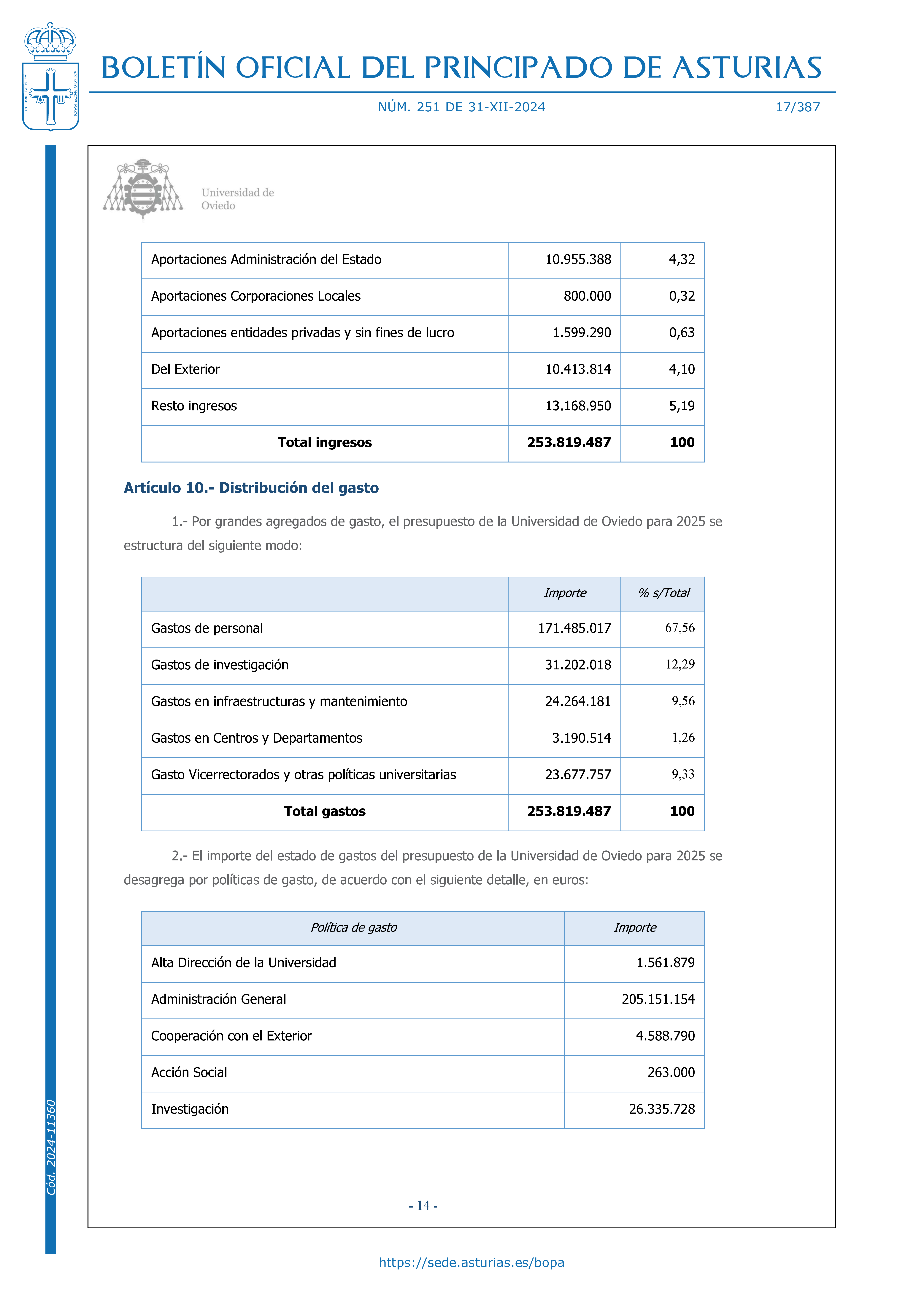
Disponemos de una imagen. En este caso se ha convertido la página 17 de los presupuestos de la Universidad de Oviedo a un formato png con resolución de 600. Como trabajo habitualmente como un ordenador con escasa memoria, debo andar con cuidado gestionando la memoria en cada paso.

file <- "https://torres.epv.uniovi.es/centon/graphics/page17_600-017.png"
image <- readPNG(file) # Lee la imagen
plot_array(image) # Dibújala
gc(verbose=FALSE) # garbage collection. We need to reserve a lot memory.

Este es la imagen que queremos procesar.

Los colores vienen descritos por tres números que varían de 0 a 1. Como ando pobre de memoria, trabajo con valores enteros. Creo una matriz auxiliar que contenga toda la información de la imagen. La imagen es un array de tres dimensiones (alto, ancho y color) y yo voy a trabajar una matriz cuyas pos posiciones se corresponden con las de la imagen. El irow y el jrow es el equivalente a la posición pos.

precision <- 1000L
dims <- dim(image)[1:2] # Dimensiones de la imagen. Es una array de tres dimensiones: largo, alto, color.
##
nms <- c("pos","irow","jcol","color_red","color_green","color_blue","color","segcolor","isbw","segbw")
##,"seglettercolor","isletter","segbw","seglettercolor","segletter","linebw","lineletters")
m <- matrix(0L,nrow=prod(dims),ncol=length(nms))
colnames(m) <-nms
gc(verbose=FALSE) # garbage collection. We need to reserve a lot memory.
## Positions as vector, as irow, and as jcol
m[,"pos"] <- seq_len(prod(dims))
m[,"irow"] <- matchmatrix:::postoirow(m[,"pos"], dims[1])
m[,"jcol"] <- matchmatrix:::postojcol(m[,"pos"], dims[1])
## Color RGB as integer.
## Check that length(dim(image)) = 3 && dim(image)[3] = 3
m[,c("color_red","color_green","color_blue")]  <- as.integer(precision*image)
gc(verbose=FALSE) # garbage collection. We need to reserve a lot memory.

En esta imagen creamos un código único para cada color que aparece. Y anotamos el código más habitual. Normalmente será el color blanco que corresponde al fondo de la imagen.

## Creamos un registro para cada color.
m[,"color"]  <-  as.integer(precision^2*m[, "color_red"] + precision*m[,"color_green"] + m[,"color_blue"])
coloresysusfrecuencias <- table2(m[,"color"]) ## Los colores más habituales y el número de píxels
## El color más habitual es el
colormashabitual <- coloresysusfrecuencias[["values"]][1]
## el color 1001001000 es el blanco, que suele ser el color de fondo.

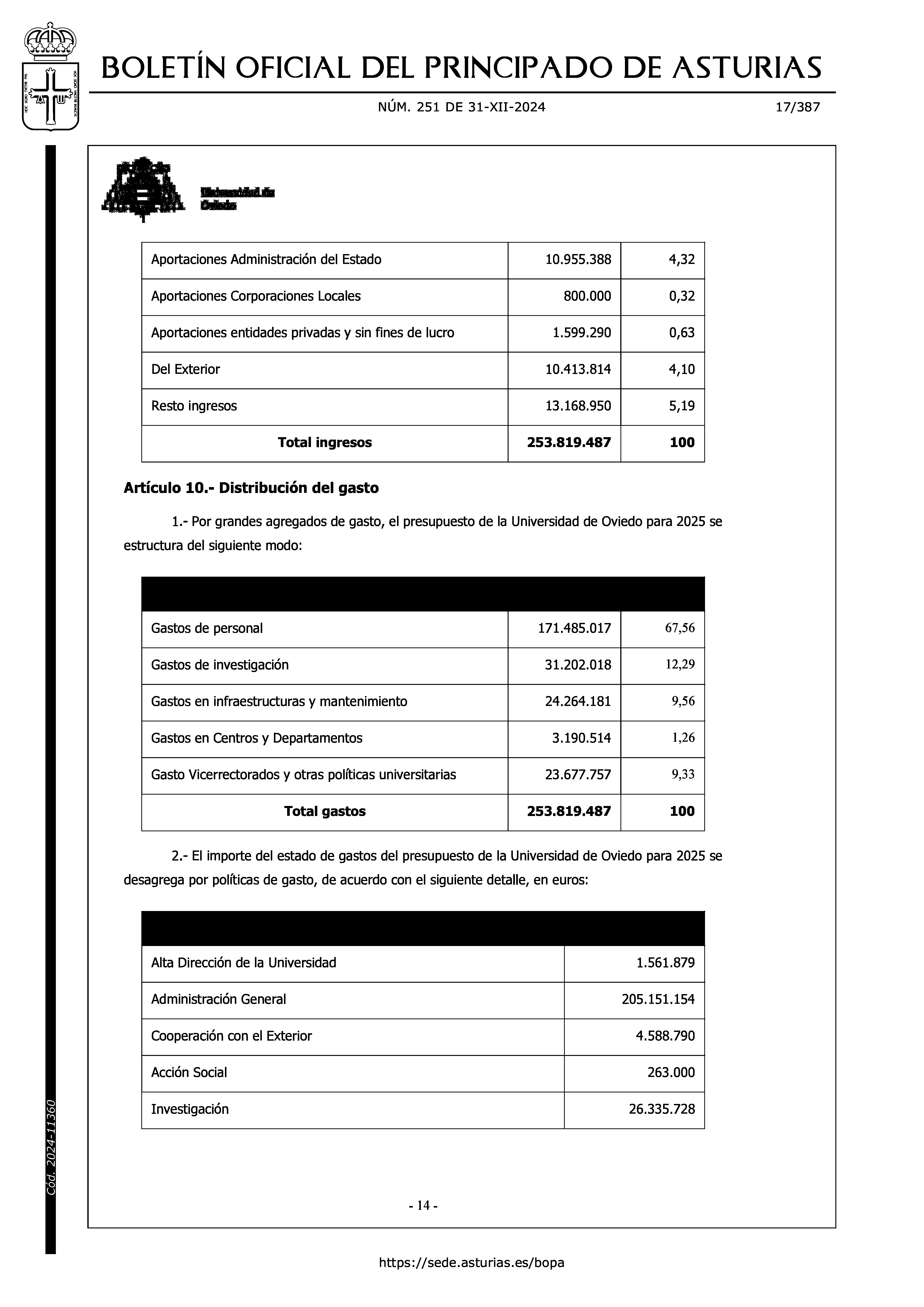
Hacemos una pequeña comprobación de los pixels que tienen este color más habitual. Creo una imagen ficticia con las mismas dimensiones que la original. La pinto de negro salvo en los pixels correspondientes al color más habitual. Como ando pobre de memoria, la guardo en el disco duro.

## Vemos cómo queda un gráfico solo con los colores de fondo.
npoints <- prod(dims)
mmask <- c(rep(0.,npoints),
           rep(0.,npoints),
           rep(0.,npoints)) ## Una imagen de color negro total.
dim(mmask) <- dim(image)
## En los puntos del este color (el fondo) cambiamos el color y
## cogemos el original
posf <- m[ m[,"color"] ==colormashabitual, "pos"]
posred <- posf
posgreen <- npoints + posf
posblue <- 2*npoints + posf
pos <- c(posred,posgreen,posblue)
mmask[pos]  <- image[pos]
writePNG(mmask,"page17_600-017-bw.png")

Como se ve, el color más predominante es el blanco, que corresponde al fondo de la página.

Ahora viene la decisión que tomé después de hacer varias pruebas sobre los colores que no son el fondo de la página. O bien considerar todos los demás colores por separado (azul, gris, negro, etc.) o bien considerarlos como del mismo color. En ese caso, me decanté por trabajar en blanco y negro. Blanco es el fondo de la página y negro representará toda la demás información. Aquí perdemos algo de información (aparece texto negro dentro de un recuadro azul y lo perdemos al considerar el color azul igual que el color negro) pero tampoco es muy relevante. En otras pruebas similares al final siempre he llegado a lo mismo: todo lo que no sea fondo de la página tiene el mismo color.

La función msegments determina qué puntos están unidos entre sí. Denomino como segmento a aquellos puntos unidos o conectados. Si dos pixels tienen el mismo segmento, están conectados.

## Trabajaremos en blanco y negro.
## Para cada color, calculamos los segmentos que contiene.
## Un segmento es una agrupación de pixels adjuntos con el mismo color.
## Solo consideramos bw
f <- m[,"color"] != colormashabitual
m[f,"segcolor"]  <- msegments(m[f,"pos"],dims) # Calculamos los segmentos

Ahora calculamos la caja (bounding box) de cada segmento mediante una función by adaptada a matrices.

## Para cada segmento de cada color, creamos
## - bounding box: xleft=, ybottom=, xright=, ytop=
## - área del boundingbox
## - pixels de ese segmento
mboundingbox <-  mdoby(m,
                       function(x){c(pixels=nrow(x),xleft=min(x[,"jcol"]),ybottom=min(x[,"irow"]),xright=max(x[,"jcol"]),ytop=max(x[,"irow"]))},
                       by=c("segcolor"),rows=NULL)

Visualizamos cómo ajusta el recuadro (bounding box) de cada segmento. Superponemos a la imagen original las cajas obtenidas.

plot_array(image)
rect(xleft=mboundingbox[,"xleft"],
     ybottom=dim(image)[1]- mboundingbox[,"ybottom"],
     xright=mboundingbox[,"xright"],
     ytop=dim(image)[1]-mboundingbox[,"ytop"],border="red",lwd=2)

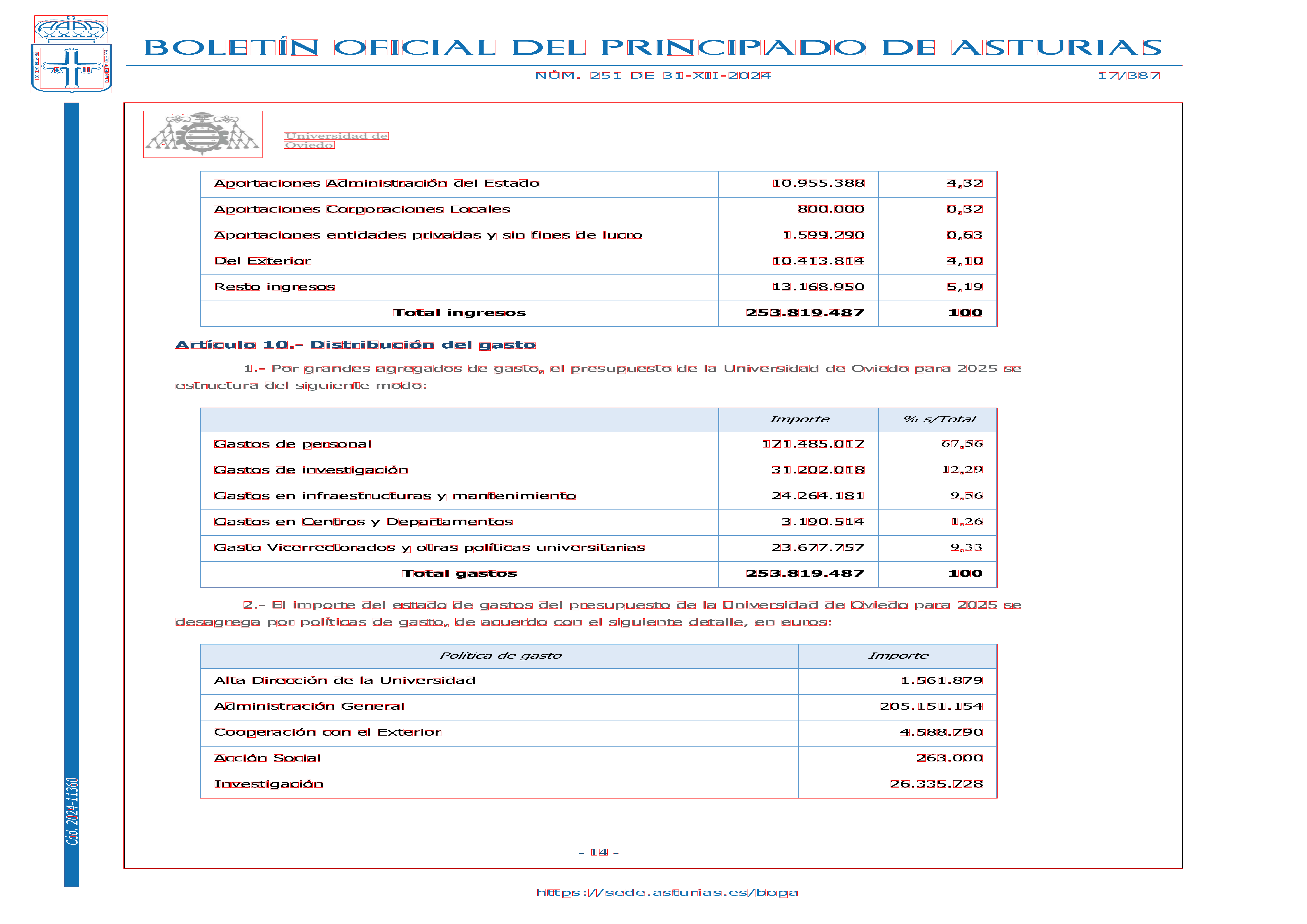
Queda bonito. Etapa superada. ¿El diligente lector puede intuir en qué consistirá el siguiente paso?