El juego del calamar y la distribución binomial

Dieciocho pasos para atravesar un puente. Igual probabilidad de vivir que de morir en cada paso. Dieciséis personas que cruzan sucesivamente el puente siguiendo la ruta trazada por sus predecesores. ¿Cuántas personas lograrán atravesar el puente?

Así es el planteamiento de la quinta prueba de la serie televisiva El juego del calamar. Hagamos un poco de cálculo de probabilidades para determinar la distribución de probabilidad del número de supervivientes.

Simulación recursiva

Seguimos los pasos sugeridos por Carlos Gil Bellosta.

jugadores <- 16
peldanos <- 18
p <- 0.5 # Probabilidad de éxito

Diseñamos una función recursiva que imite el comportamiento del juego. Empiezan n personas que tienen que recorrer m peldaños. Si el azar les sonríe, en cada paso avanza un peldaño, quedando m-1 peldaños por recorrer. Si el azar les perjudica, avanzan un peldaño, por lo que les quedan m-1, a costa de eliminar un jugador, y siguen el juego n-1 personas.

foo <- function(n, m){
  if (m == 0 || n == 0)
      return(n)
  if (rbinom(1, 1, p) == 1)
    return(foo(n, m - 1))
  else
    return(foo(n-1, m - 1))
}

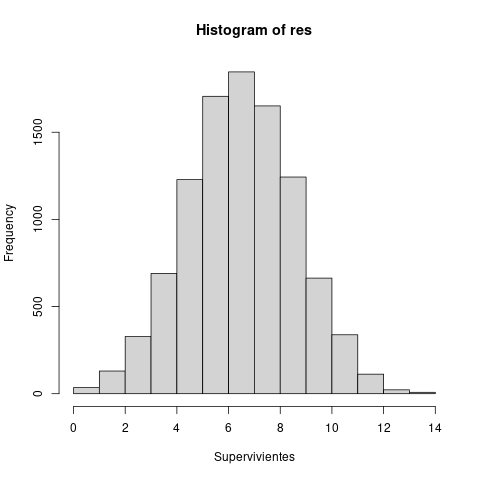
Y ahora, la simulación, con res el número de personas que sobreviven al juego.

set.seed(123)
res <- replicate(10000,foo(jugadores, peldanos))
table(res)

res
   0    1    2    3    4    5    6    7    8    9   10   11   12   13   14 
   6   29  130  328  690 1228 1706 1846 1651 1243  663  338  112   22    8

hist(res,xlab="Supervivientes")

Distribución binomial

Inicialmente leí el trabajo de JJAlcalde74, que plantea el problema utilizando una distribución binomial. Me planteé resolver este problema resolviéndolo como una distribución binomial negativa, pero es mucho más fácil siguiendo el razonamiento de JJAlcalde74.

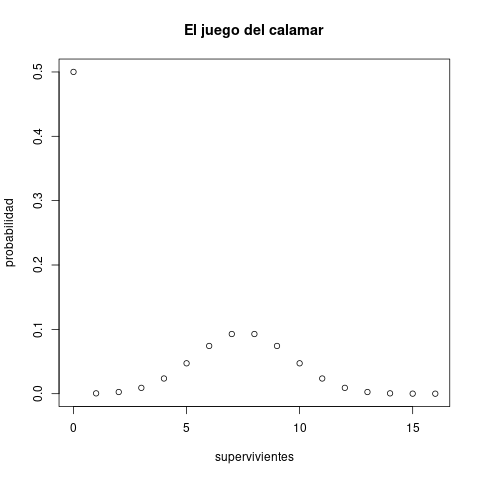
Sea Y el número de peldaños rotos en un puente con 18 peldaños cuando se prueban todos ellos. La probabilidad de rotura de cada peldaño es 0.5 y es independiente del resto. Entonces Y sigue una distribución binomial Binomial(n=18, p=0.5) con Y = 0,1,2,…,18. Calculemos cuánto valen estas probabilidades.

jugadores <- 16
peldanos <- 18
p <- 0.5 # Probabilidad de éxito

y <- 0:peldanos
(probsy <- dbinom(y,size=peldanos,prob=p))

 [1] 3.814697e-06 6.866455e-05 5.836487e-04 3.112793e-03 1.167297e-02
 [6] 3.268433e-02 7.081604e-02 1.213989e-01 1.669235e-01 1.854706e-01
[11] 1.669235e-01 1.213989e-01 7.081604e-02 3.268433e-02 1.167297e-02
[16] 3.112793e-03 5.836487e-04 6.866455e-05 3.814697e-06

Sea X el número de muertos según las reglas del juego. Entonces X = min(Jugadores, Y). Es decir, es la distribución truncada de Y.

x <- 0:jugadores
(probabilidad <- c(probsy[y < jugadores], sum(probsy[y>=jugadores])))

 [1] 3.814697e-06 6.866455e-05 5.836487e-04 3.112793e-03 1.167297e-02
 [6] 3.268433e-02 7.081604e-02 1.213989e-01 1.669235e-01 1.854706e-01
[11] 1.669235e-01 1.213989e-01 7.081604e-02 3.268433e-02 1.167297e-02
[16] 3.112793e-03 6.561279e-04

Dibujemos la distribución de la probabilidad de que sobrevivan los jugadores.

supervivientes <- jugadores-x
plot(supervivientes,probabilidad,main="El juego del calamar")