Contraste de proporciones y validación de un modelo con R

Pidió a su cliente que dividiera su base de datos en dos grupos al azar para verificar la bondad de un modelo. Como el divulgador ya era perro viejo, dudó del proceso de partición de los datos y revisó la proporción de éxitos en cada grupo:

• Grupo A: 119\(\,\)072 éxitos en 363\(\,\)523 sujetos (32.75%).
• Grupo B: 118\(\,\)713 éxitos en 372\(\,\)664 sujetos (31.85%).

n1 <- 363523
n2 <- 372664
op1 <- 119072
op2 <- 118713
(dif <- op1/n1 -op2/n2)

[1] 0.008997745

Existía una diferencia de menos del 1% entre ambas proporciones. Si el cliente dio por buena dicha separación, implicaba que el tamaño del efecto deviene irrelevante. El refrán «Donde manda capitán, no manda marinero» se impuso y tocó validar el modelo.

Empero, el consultor reflexiona en voz alta:

Sin embargo, no hemos visto el código con el que se ha realizado la partición. Además, tenemos motivos (¿sobrados?) para sospechar lo pésimo. No tenemos una priori sobre la probabilidad de que el muestreo esté correctamente realizado, pero la posteriori, a la vista de los datos, es necesariamente minúscula.

Revisemos si ambas proporciones son iguales o no mediante un contraste de proporciones

Acudimos al test clásico de proporciones para resolver este contraste:

prop.test(c(op1,op2),c(n1,n2))

	2-sample test for equality of proportions with continuity correction

data:  c(op1, op2) out of c(n1, n2)
X-squared = 68.089, df = 1, p-value < 2.2e-16
alternative hypothesis: two.sided
95 percent confidence interval:
 0.006858391 0.011137098
sample estimates:
   prop 1    prop 2 
0.3275501 0.3185524

El intervalo de confianza para la diferencia de proporciones no contiene al cero y además el p-valor minora la precisión del ordenador. El test de proporciones utiliza la distribución normal.

Repetimos el estudio mediante el remuestreo. Calculamos el intervalo de confianza de nuevo.

v1 <- rep(0L, n1)
v1[1L:op1] <- 1L
v2 <- rep(0L, n2)
v2[1L:op2] <- 1L

## Confidence Interval
set.seed(123)
resconf <- replicate(100, {
    tmp1 <- sample(v1, length(v1), replace =TRUE)
    tmp2 <- sample(v2, length(v2), replace =TRUE)
    mean(tmp1) -mean(tmp2)
})

quantile(resconf,c(0.025,0.975))

       2.5%       97.5% 
0.007012723 0.010815158

El intervalo de confianza al 95% para la diferencia de proporciones varía del 0.7% al 1.0%. El p-valor determina la probabilidad de obtener una muestra peor de cara a no rechazar la hipótesis nula cuando ésta es cierta. Bajo la veracidad de la hipótesis nula, ambos grupos provienen de la misma población.

## H_0: Data comes from the same distribution
population <- c(v1, v2)
set.seed(456)
res <- replicate(100, {
    tmp1 <- sample(population, n1, replace =TRUE)
    tmp2 <- sample(population, n2, replace =TRUE)
    mean(tmp1) -mean(tmp2)
})

hist(res,xlim=c(min(res,-dif),max(res,dif)))
abline(v = -abs(dif), col = "red")
abline(v = abs(dif), col = "red")

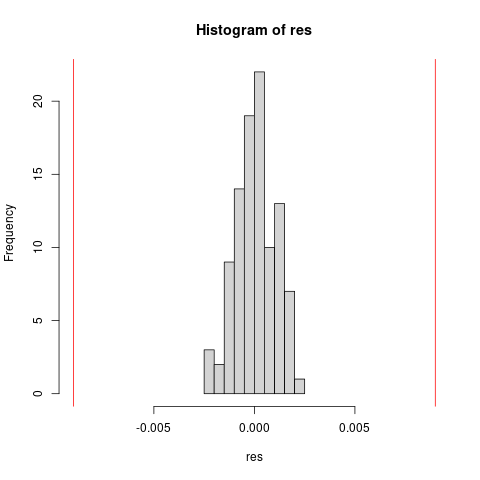
La diferencia observada en los datos resulta excesiva bajo el supuesto de que los datos provengan de una misma población.

sum(res < -abs(dif) | res > abs(dif))/length(res) # p-value

[1] 0

Acabamos de calcular la «probabilidad de obtener una desproporción como la que muestran los datos suponiendo que la partición sea perfectamente aleatoria», más conocido con el nombre de p-valor. Y añade el consultor bajo un enfoque bayesiano «Pero sabemos poco acerca de la recíproca: no conocemos la probabilidad de que la partición sea perfectamente aleatoria a la vista de la obtenida».

¿Cómo afecta al modelo estimado el hecho de que ambos grupos provengan de dos poblaciones distintas? Si el modelo se diseña para el grupo A, ¿valdrá este modelo para el grupo B? o ¿siquiera debe aplicarse al grupo B? ¿Cuál ha de ser el criterio de validación?

¡Menuda incertidumbre! Malhadada vida la del mundano estadístico.

• P-valores y decisiones.