Tamaño del conjunto de entrenamiento versus el de validación

Resulta habitual dividir el conjunto de datos disponibles en dos partes, una de entrenamiento y otra para validar los resultados. Surge la duda de cuál deviene la proporción más adecuada para separar el conjunto de entrenamiento del de validación: ¿que cada grupo contenga la mitad de los datos? ¿que las proporciones se sitúen en el 70% y 30%, respectivamente? ¿existe alguna regla para delimitar dichas cantidades?

Adoración de los Reyes Magos, Diego Rodríguez de Silva y Velázquez.

La referencia citada por Jose Luis Cañadas inspira esta entrada. Generamos diez mil datos de una distribución normal de media cero y desviación típica la unidad.

set.seed(123)
n <- 10^4
x <- rnorm(n,0,1)

¿Qué ocurre con una proporción de 70%-30%?

Dividimos el conjunto en dos partes, una denominada entrenamiento, train, y la otra validación, test. En el primer ejemplo, el 70% de los datos será de entrenamiento. Seleccionamos al azar los conjuntos de entrenamiento y validación. Calculamos la media y la desviación típica del conjunto de entrenamiento. Anotamos el p-valor del test de Kolmogorov-Smirnov cuando testeamos si los datos de validación siguen una distribución normal con la media y desviación típica del conjunto de entrenamiento.

  getpvalue <- function(proportion){
      ## Split the original data into train and test data sets.
      postrain <- sample(1:n,n*proportion)
      xtrain <- x[postrain]
      xtest <- x[-postrain]

      ## Compute the mean and standard deviation of the train data
      meantrain <- mean(xtrain)
      sdtrain <- sd(xtrain)

      ## Check normaility of the test data
      pvalue <- ks.test(xtest,"pnorm",meantrain,sdtrain)$p.value
      pvalue
  }

getpvalue(0.7)

[1] 0.1834823

Repetimos este proceso mil veces y dibujamos los p-valores obtenidos. Asimismo, contamos cuántas veces aparece un p-valor inferior al 5%.

rp <-   replicate(1000, getpvalue(0.7))
print(100*sum(rp < 0.05) / length(rp))
hist(rp)

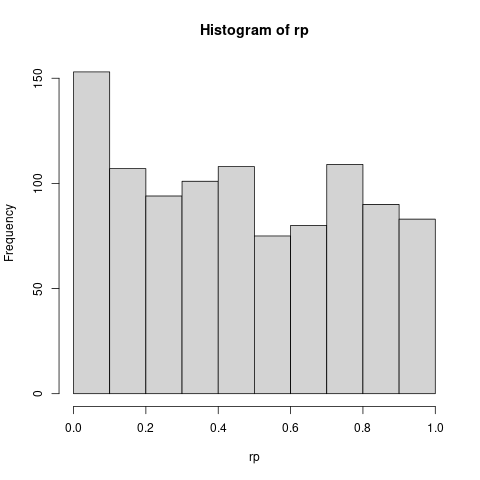
Aproximadamente, en el 7.9% de las veces obtenemos un p-valor inferior al 5%. Hasta ahora hemos utilizado una proporción de 70% y 30% para el conjunto de entrenamiento y de validación, respectivamente. ¿Qué ocurre si modificamos esta proporción?

¿Qué ocurre con una proporción arbitraria?

Repetimos el experimento variando la proporción y anotamos el porcentaje de p-valores inferiores al 5% que aparecen. Las proporciones variarán desde considerar la mitad de los datos como entrenamiento (el 50%) hasta emplear casi toda la base de datos como entrenamiento (el 99%).

 proporciones <- c(50:99)/100
vecesmenoresqueelcinco <-  sapply(proporciones, function(proportion){
     rp <-   replicate(1000,getpvalue(proportion))
     100*sum(rp < 0.05) / length(rp)
 } )

 plot(100*proporciones,vecesmenoresqueelcinco,
      xlab="Proporción de datos en el conjunto de entrenamiento",
      ylab="Porcentaje de veces que aparece un p-valor menor del 5%")

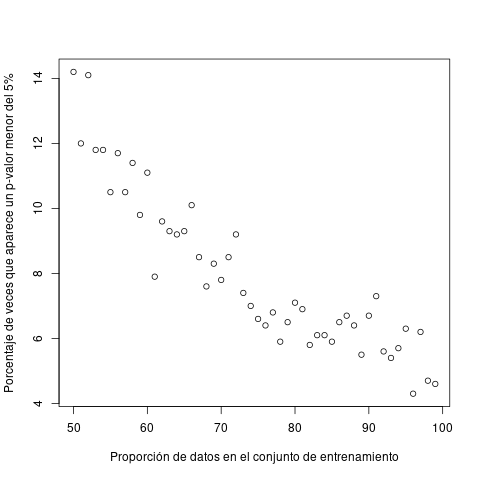
Si examinamos el dibujo, cuando cogemos la mitad de los datos como entrenamiento y la otra mitad para validar (50%-50%), en el 12% de las veces el p-valor minora al 5%. Para una proporción de 70% de datos de entrenamiento y 30% de datos de validación, los p-valores inferiores al 5% son el 7.7%, mientras que si la proporción de entrenamiento supera el 95%, entonces el porcentaje de p-valores inferiores al 5% es menor del 5%.

Moraleja

Moraleja: si desea dividir su conjunto de datos en uno de entrenamiento y otro de validación, efectúe antes alguna simulación sencilla para intuir con qué resultados se puede encontrar.

Referencia

Arthur Charpentier Lilliefors, Kolmogorov-Smirnov and cross-validation.