Simulación y la Ley 0-1 de Kolmogorov
2025-11-03
Simulación y la Ley 0-1 de Kolmogorov
En ciertos ámbitos, tanto académicos como industriales, se comprueban determinados comportamientos mediante simulación. Si bien esta aproximación resulta sencilla y fácil de aplicar, no siempre produce el resultado esperado. La Ley 0-1 de Kolmogorov así lo establece.
Calcular la media de una distribución uniforme mediante simulación
La variable aleatoria que sigue una distribución uniforme Uniforme(0,1) tiene una media de 0.5 y una varianza de 1/12. En vez de demostrar estas propiedades, realizamos dos simulaciones para comprobar estos resultados.
En la primera simulación fijamos una semilla, simulamos 100 observaciones de una distribución uniforme y calculamos la media y la varianza de los datos.
set.seed(123) x <- runif(100) cat("La media es",mean(x),"\n") cat("La varianza es",mean( (x-mean(x))^2),"\n")
La media es 0.498559 La varianza es 0.08041008
En el ejemplo anterior, más o menos la media y la varianza coinciden con el resultado teórico.
Repitamos este experimento fijando otra semilla aleatoria y generando otros 100 valores pseudo aleatorios.
set.seed(5182480) x <- runif(100) cat("La media es",mean(x),"\n") cat("La varianza es",mean( (x-mean(x))^2),"\n")
La media es 0.3435172 La varianza es 0.05990992
En este caso, la media y la varianza difieren considerablemente del resultado teórico. Y difícilmente su histograma se puede considerar como una distribución uniforme.
hist(x)
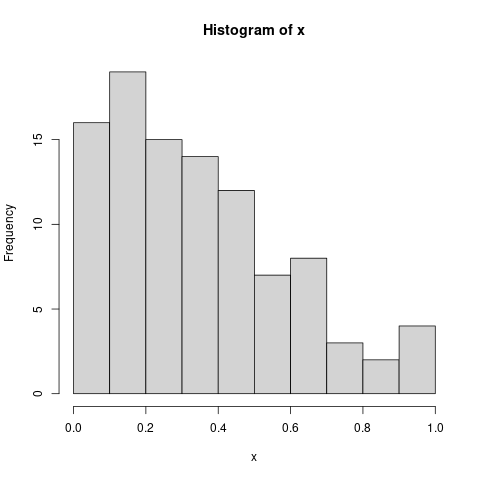
La simulación es conveniente pero no infalible
En el último ejemplo se acaba de producir una aplicación de la Ley 0-1 de Kolmogorov, que señala que si se repite las veces necesarias un experimento que contenga un evento con probabilidad no nula, éste se acaba produciendo.
Por lo tanto, la simulación deviene en una herramienta muy útil sabiendo que de vez en cuando proporciona resultados extraños.