Constrate de la velocidad media de la luz con R
2025-11-03
Constrate de la velocidad media de la luz con R
En 1882 Simon Newcomb midió la velocidad de la luz. Anotó el tiempo que tardaba en recorrer la distancia entre un punto y un espejo, que entre ida y vuelta suma en total 7\(\,\)442 metros. En las unidades anotadas, actualmente existe el consenso de que la velocidad de la luz es de 33.02 unidades (para pasar estas unidades a millonésimas de segundo, multiplique por 10-3 y sume 24.8).
No me mueve, mi Dios, para quererte
el cielo que me tienes prometido,
ni me mueve el infierno tan temido
para dejar por eso de ofenderte.
¡Tú me mueves, Señor! Muéveme el verte
clavado en una cruz y escarnecido;
muéveme ver tu cuerpo tan herido;
muévenme tus afrentas y tu muerte.
Muéveme en fin, tu amor, y en tal manera
que aunque no hubiera cielo, yo te amara,
y aunque no hubiera infierno, te temiera.
No me tienes que dar porque te quiera,
pues aunque lo que espero no esperara,
lo mismo que te quiero te quisiera.

Deseamos saber si el experimento de Newcomb confirma la vigente creencia de que la luz viaja a 33.02 unidades. La hipótesis nula y la alternativa quedan de la siguiente forma:
\begin{cases} H_{0}:\: \mu = 33.02 \cr H_{1}:\: \mu \not= 33.02 \cr \end{cases}
Su experimento consta de sesenta y seis observaciones que vienen recogidas en el paquete MASS de R bajo la denominación de newcomb.
newcomb <- c(28, -44, 29, 30, 24, 28, 37, 32, 36, 27, 26, 28, 29, 26, 27,
22, 23, 20, 25, 25, 36, 23, 31, 32, 24, 27, 33, 16, 24, 29, 36,
21, 28, 26, 27, 27, 32, 25, 28, 24, 40, 21, 31, 32, 28, 26, 30,
27, 26, 24, 32, 29, 34, -2, 25, 19, 36, 29, 30, 22, 28, 33, 39,
25, 16, 23)
hist(newcomb)
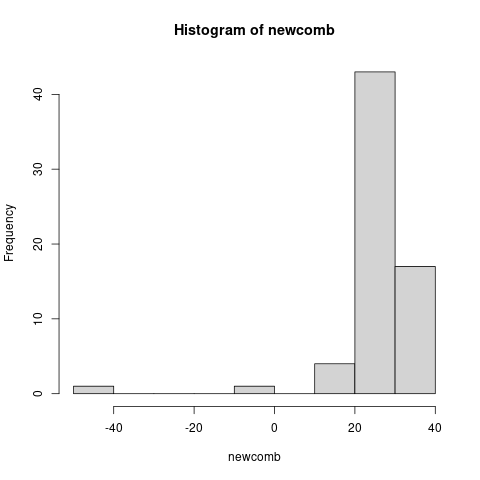
Parece claro que estos datos no siguen una distribución normal. Existen dos observaciones (-44 y -2) que destacan claramente. Tal vez habría que revisar las condiciones de esas mediciones y determinar si se eliminan o no del estudio.
Análisis con todos los datos del estudio
Como contamos con sesenta y seis observaciones, el Teorema Central del Límite apunta a normalidad del promedio, por lo que hacemos el test t de Student.
t.test(newcomb,mu=33.02)
One Sample t-test data: newcomb t = -5.1471, df = 65, p-value = 2.648e-06 alternative hypothesis: true mean is not equal to 33.02 95 percent confidence interval: 23.57059 28.85365 sample estimates: mean of x 26.21212
Los resultados indican que la media muestral vale 26.21, el intervalo de confianza al 95% para la media poblacional varía entre 23.5 y 28.85, mientras que el p-valor disminuye hasta 2.648e-06. Parece que los datos del experimento de Newcomb no avalan que la velocidad alcance las 33.02 unidades.
Sin embargo, al encontrar unos datos tan distanciados de la distribución normal, surge la duda de si realmente sesenta y seis observaciones representa un tamaño suficiente para que el Teorema Centra del Límite converja. En realidad, este teorema requiere que el tamaño tienda a infinito. Por precaución, implementamos la versión bootstrap o remuestreo para estas hipótesis. Empecemos con el intervalo de confianza para la media.
set.seed(546) btmean <- replicate(1000,{ y <- sample(newcomb,length(newcomb),replace=TRUE) mean(y) }) quantile(btmean,probs=c(0.025,0.975))
2.5% 97.5%
23.25682 28.34886
Sale muy parecido al del test t.
Determinemos el p-valor. El p-valor representa la probabilidad de ocurrir un resultado igual o peor al obtenido suponiendo la veracidad de la hipótesis nula. La hipótesis nula indica que la media verdadera se sitúa en 33.02, por lo que hemos de ajustar los datos para que tomen esta media. Unas sencillas restas y sumas crean un nuevo conjunto de datos con esta media.
mu <- 33.02 mean(newcomb) newcombh0 <- newcomb - mean(newcomb) + mu mean(newcombh0) (dif <- abs(mean(newcombh0) - mean(newcomb)))
[1] 26.21212 [1] 33.02 [1] 6.807879
La distancia de la media muestral a la media poblacional se sitúa en 6.8. Por lo tanto, la probabilidad p-valor de que ocurran eventos más desfavorables surge de o bien obtener resultados menores que 26.21 (33.02- 6.8), o bien resultados mayores que 39.82 (33.02 + 6.8).
Con los datos ya ajustados según la hipótesis nula, procedemos al remuestreo, repitiendo el procedimiento mil veces.
set.seed(789) bstrpmeanh0 <- replicate(1000,{ y <- sample(newcombh0,length(newcombh0),replace=TRUE) mean(y) }) hist(bstrpmeanh0)
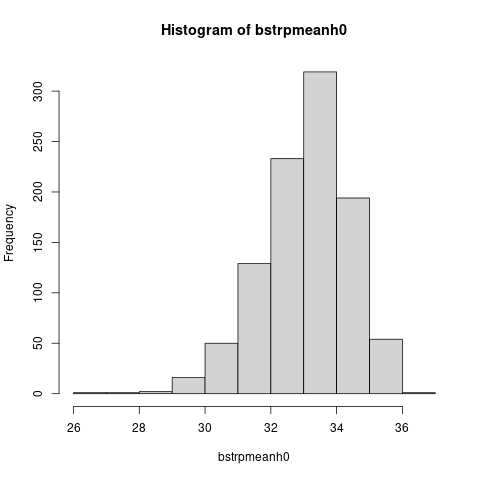
Y nos queda calcular el p-valor, que en este caso vale cero.
sum( bstrpmeanh0 < mu - dif | bstrpmeanh0 > mu + dif) / length(bstrpmeanh0)
[1] 0
Por lo tanto, el experimento de Newcomb concluye que la velocidad de la luz no es 33.02.
Eliminación de las observaciones atípicas
La inspección visual de los datos mostró dos valores negativos muy diferentes del resto. Sin conocer las condiciones de la medición, no sabemos la fiabilidad de la misma. Por si acaso, repitamos el estudio sin considerar esos valores atípicos.
depunewcomb <- newcomb[ newcomb > 0]
hist(depunewcomb)
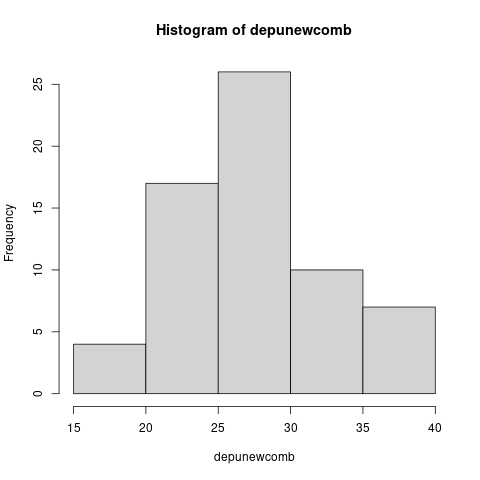
El histograma sí parece acampanado. Para comprobar la normalidad, realizamos el gráfico cuantil cuantil, que disipa nuestras dudas sobre las condiciones de normalidad de estos datos depurados.
library(car)
qqPlot(depunewcomb)
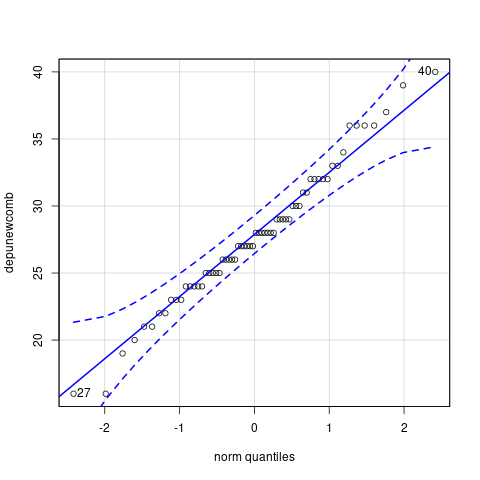
Repetimos los pasos de la sección anterior aplicándolos a los datos depurados. En primer lugar, el test t.
t.test(depunewcomb)
One Sample t-test
data: depunewcomb
t = 43.671, df = 63, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
26.4802 29.0198
sample estimates:
mean of x
27.75
Hagamos el análisis de remuestreo. El intervalo de confianza queda
set.seed(561) depubtmean <- replicate(1000,{ y <- sample(depunewcomb,length(depunewcomb),replace=TRUE) mean(y) }) quantile(depubtmean,probs=c(0.025,0.975))
2.5% 97.5%
26.49922 29.03164
mientras que el p-valor vale cero.
mu <- 33.02 depunewcombh0 <- depunewcomb - mean(depunewcomb) + mu dif <- abs(mean(depunewcombh0) - mean(depunewcomb)) set.seed(789) depubstrpmeanh0 <- replicate(1000,{ y <- sample(depunewcombh0,length(depunewcombh0),replace=TRUE) mean(y) }) sum( depubstrpmeanh0 < mu - dif | depubstrpmeanh0 > mu + dif) / length(depubstrpmeanh0)
[1] 0
Por lo tanto, según el experimento de 1882 de Simon Newcomb, no aceptamos como verdadera la vigente creencia de que la luz viaje a 33.02 unidades.
Conclusión
Lo que hoy rezuma certeza, mañana deviene en falsedad. Aprendamos a manejar la incertidumbre. Quién sabe dónde estaremos mañana: «Porque ni del sabio ni del necio habrá memoria para siempre; pues en los días venideros ya todo será olvidado, y también morirá el sabio como el necio» (Eclesiastés 2, 16).
Referencias
- Simon Newcomb. Simon Newcomb fue el descubridor de la ley de números raros de Benford, que se utiliza actualmente para detectar fraudes contables.
Una introducción a los contrastes de hipótesis
Esta entrada forma parte de un serie de artículos introductorios sobre contrastes de hipótesis: