Contraste de normalidad con R
2025-11-03
Contraste de normalidad con R
La distribución normal constituye el fundamento de la inferencia estadística. Numerosas propiedades se basan en que la muestra aleatoria simple provenga de una distribución normal. Dependiendo del origen de los datos, en unas situaciones las observaciones provienen claramente de una distribución normal (normalmente en experimentos en ambientes controlados), mientras que en otras apenas habrá rastro de normalidad.

Aunque no exista la normalidad en los datos, el Teorema Central de Límite garantiza que bajo ciertas condiciones muy generales y si el tamaño muestral alcanza determinadas magnitudes, los promedios sí se comportan bajo condiciones de normalidad.
La gráfica de la distribución normal
La gráfica de la distribución normal presenta un forma acampanada, simétrica respecto a su media.
library(ggplot2) ggplot(data.frame(x = c(0, 1)), aes(x = x)) + stat_function(fun = dnorm, args = list(0, 1), aes(colour = "$\\mu=0,\\,\\sigma=1$")) + stat_function(fun = dnorm, args = list(3, 1), aes(colour = "$\\mu=3,\\,\\sigma=1$")) + stat_function(fun = dnorm, args = list(-3, 3), aes(colour = "$\\mu=-3,\\,\\sigma=3$")) + ggtitle("Distribuci\\'on Normal") + scale_colour_brewer(palette="Accent") + labs(colour = "Normal") + scale_x_continuous(name="$x$",expand = c(0, 0),limits=c(-10,8)) + scale_y_continuous(name = "Funci\\'on de densidad $f(x)$",expand = c(0, 0),limits=c(0,NA))+ theme_classic()
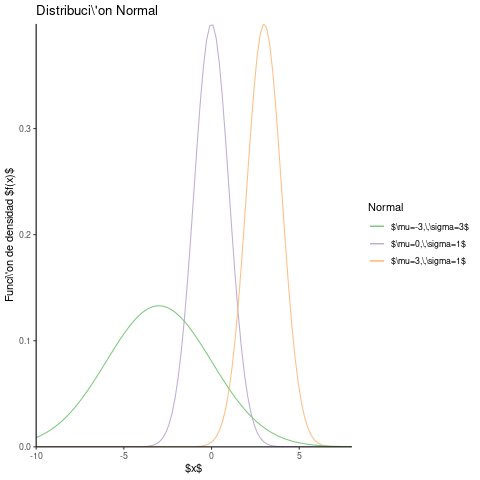
Esta simetría implica que la mediana y la media coincide. Si no coinciden o se encuentran alejadas, conviene revisar la presencia de algún dato atípico que contamina la media.
Un experimento recogió y midió las longitudes de los pétalos de tres especies florales. Los datos aparecen recopilados en la base de datos iris. Estudiemos la normalidad de esta magnitud.
data(iris) hist(iris$Petal.Length)
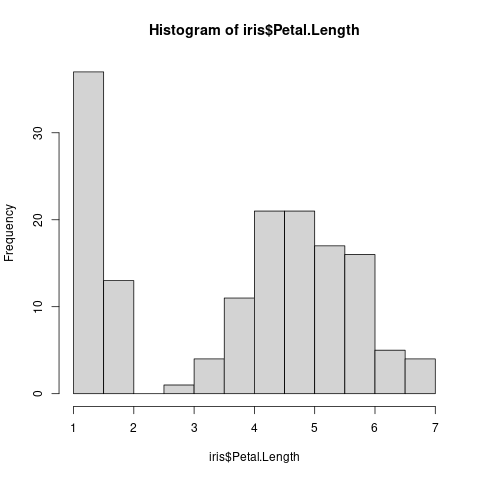
Parece que concurren un importante número de observaciones en torno al valor uno con un comportamiento bastante diferente al resto. La distribución Tweedie o los modelos cero-inflados como alternativas a la distribución normal se convierten en una opción razonable. O bien realizar alguna transformación de los datos de tipo logarítmico o transformación de Box-Cox.
Antes de aventurarme a tan procelosa tarea, rememoro las enseñanzas de Feynman y reviso con calma este experimento: análisis métrico de tres variedades de una flor. Tal vez la magnitud que estudiamos, la longitud de pétalo, forme parte de las características diferenciadoras de cada especie. Parece razonable intuir que el diferente comportamiento en las mediciones observadas se deba al tipo de flor. Representamos la distribución de los datos de acuerdo a la especie a la que pertenece.
ggplot(iris, aes(x = Petal.Length,color=Species)) +
geom_density()+
scale_colour_brewer(palette="Accent") +
labs(colour = "Especies") +
scale_x_continuous(name="Petal.Length",expand = c(0, 0)) +
scale_y_continuous(name = "Funci\\'on de densidad $f(x)$",expand=c(0,0),limits=c(0,NA))+
theme_classic()
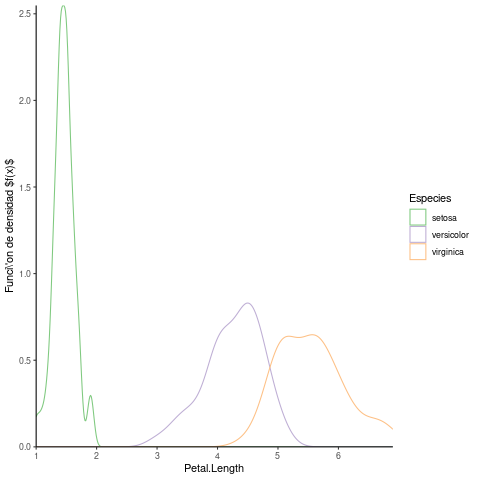
Parece que cada especie de la flor muestra un comportamiento diferenciado. Examinémoslas por separado.
tapply(iris$Petal.Length,iris$Species, summary)
$setosa Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.400 1.500 1.462 1.575 1.900 $versicolor Min. 1st Qu. Median Mean 3rd Qu. Max. 3.00 4.00 4.35 4.26 4.60 5.10 $virginica Min. 1st Qu. Median Mean 3rd Qu. Max. 4.500 5.100 5.550 5.552 5.875 6.900
En cada grupo, la mediana y la media se acercan bastante.
El gráfico cuantil-cuantil
El gráfico cuantil-cuantil muestra puntos alienados cuando los datos siguen una distribución normal. Examinemos dicho gráfico para cada especie. Empecemos con la especie setosa.
xsetosa <- iris$Petal.Length[iris$Species=="setosa"] library(car) qqPlot(xsetosa)
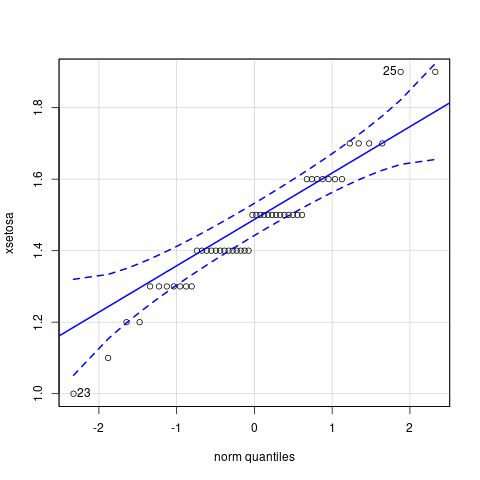
Dado que existe poca granularidad en los datos, algunos puntos aparecen alineados de forma horizontal. La suerte en este caso reside en que se ubican dentro del intervalo de confianza. Procedemos de forma similar con las otras especies. A ojo de buen cubero, parece que los datos sí entran dentro de los intervalos de confianza.
xversicolor <- iris$Petal.Length[iris$Species=="versicolor"] qqPlot(xversicolor)
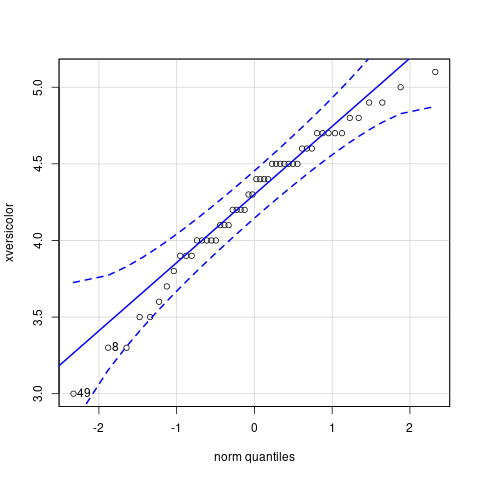
xvirginica <- iris$Petal.Length[iris$Species=="virginica"] qqPlot(xvirginica)
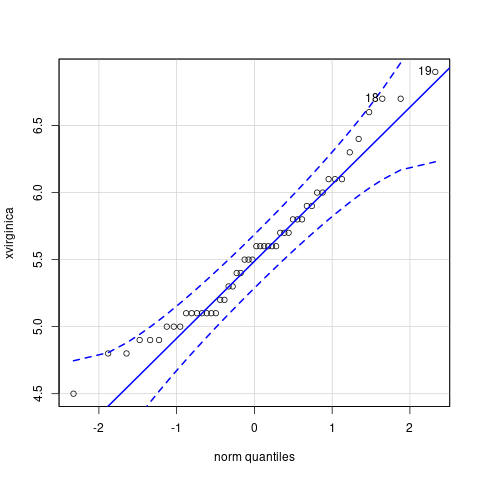
Test de Shapiro-Wilk
Una vez procesados y examinados los gráficos, empleamos el test de Shapiro-Wilk para contrastar la hipótesis nula de normalidad. Lo aplicamos a cada especie por separado.
tapply(iris$Petal.Length,iris$Species,shapiro.test)
$setosa Shapiro-Wilk normality test data: X[[i]] W = 0.95498, p-value = 0.05481 $versicolor Shapiro-Wilk normality test data: X[[i]] W = 0.966, p-value = 0.1585 $virginica Shapiro-Wilk normality test data: X[[i]] W = 0.96219, p-value = 0.1098
Parece que los p-valores no indican excesiva discrepancia de los datos con la hipótesis de normalidad. En la especie setosa se debe sobre todo a que aparecen muchos valores duplicados (poca granularidad), alejándose por tanto del concepto de variable continua, donde habitualmente no se repiten valores.
Con estos datos, la hipótesis de normalidad en cada especie es consistente.
¿Y si se hubiera rechazado la hipótesis de normalidad?
La suerte ha salido a nuestro encuentro: la normalidad inunda las situaciones cotidianas de nuestra vida. Sobre todo si medimos la longitud de los pétalos florales de una determinada especie.
Pero, ¿y si no hubiéramos conocido que esa información proviene de tres especies distintas? En tal caso, existen varias opciones.
Repesemos el experimento: ¿existen valores atípicos? ¿el experimento se ha diseñado correctamente? ¿se han transcrito erróneamente los datos? ¿se han producido sesgos en la recogida de los mismos? ¿los datos concuerdan con algún modelo teórico? ¿damos por buena la calidad de la información recogida?
¿Necesito la normalidad? Cuando el tamaño de muestra es suficientemente grande, gran parte de los estadísticos aprovechan el Teorema Central del Límite, que establece que los promedios siguen una distribución normal.
¿Normalidad en esta situación? Dependiendo de la naturaleza del experimento, conviene emplear distintas distribuciones. En el caso de tiempos de espera, la gamma, en casos de conteos, la de Poisson, o de forma general, la Tweedie. Todas ellas representan distribuciones que ajustan mejor los datos que una distribución normal en determinadas circunstancias.
¿Transformación de los datos? A veces, basta emplear una transformación logarítmica para obrar milagros. Las transformaciones de Box-Cox aportan un método sistemático para realizar tales conjuros.
¿Los datos no son independientes? Si existen correlaciones entre ellos, tal vez convenga incluir esta dependencia en nuestro estudio.
Conclusión
La distribución normal alcanza el culmen de las distribuciones estadísticas. Sus propiedades reflejan muy adecuadamente la realidad. Una inspección visual, una depuración previa o bien una segmentación afloran la naturaleza normal de la realidad. Y aunque no aflore, el Teorema Central del Límite asegura que sí existe la normalidad en un gran número de observaciones independientes.
Referencias
- Richard P. Feynman, Cargo Cult Science.
- Teorema Central del Límite. El Teorema Central del Límite indica que, en condiciones muy generales, si \(S_{n}\) es la suma de \(n\) variables aleatorias independientes, idénticamente distribuidas y de varianza no nula pero finita, entonces la función de distribución de \(S_{n}\) «se aproxima bien» a una distribución normal. En roman paladino, si en nuestro experimento las observaciones son independientes y se pueden sumar, esta suma sigue una distribución normal.
Una introducción a los contrastes de hipótesis
Esta entrada forma parte de un serie de artículos introductorios sobre contrastes de hipótesis: