La trampa del p-valor

Dicen que la constancia y el trabajo duro preceden al éxito en la investigación científica. Un científico reflexiona sobre si merece la pena repetir y repetir un experimento hasta encontrar el resultado deseado. La duda de si tanto esfuerzo servirá para algo le corroe. La desdicha o la gloria le esperan. ¿Cuál saldrá a su encuentro?

La caída de los ángeles rebeldes.

Planteemos una simulación que refleje tan incierta ventura. Repitamos mil veces el mismo protocolo. Éste consiste en cien mediciones del grosor de los huesos de ratones a los que se inyectan corticoides. Deseamos saber si los resultados se ajustan a una distribución normal. En cada experimento, aplicamos el test de Shapiro-Wilk y anotamos el p-valor.

set.seed(222)
pvals <- replicate(1000,{
    x <- rnorm(100,mean=34,sd=3)
    shapiro.test(x)$p.value
})
hist(pvals)

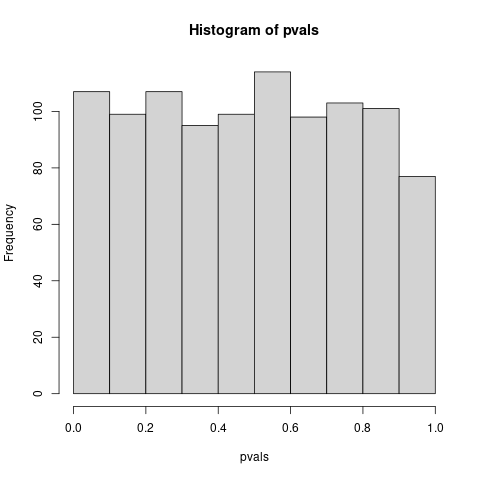
El histograma de los mil p-valores obtenidos muestra p-valores en todo el rango entre cero y uno. Se asemeja demasiado a una distribución uniforme. Dibujamos el gráfico cuantil-cuantil con la distribución uniforme y los p-valores recopilados.

library(car)
qqPlot(pvals, distribution="unif")

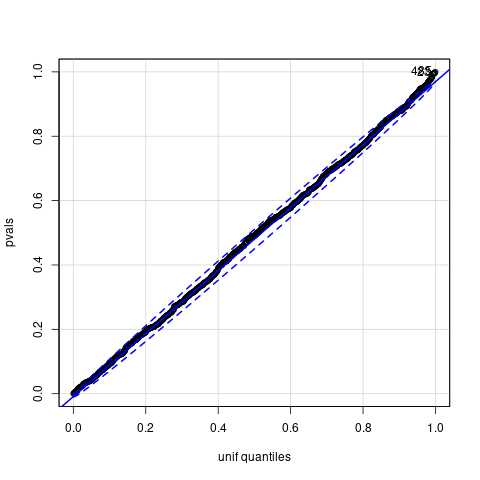
¡Un gráfico de libro! Los p-valores obtenidos en los mil experimentos ¡siguen una distribución uniforme!

Y ahora, la explicación: «Este gráfico pone de manifiesto que los p-valores obtenidos siguen una ley uniforme (en [0,1]) tal y como cabe esperar de la teoría. Porque el p-valor no es otra cosa que \(F^{-1}(X)\) donde en este caso, bajo la hipótesis nula, \(X\) tiene la distribución dada por \(F\)».

O en román paladino, probado un número suficiente de experimentos, siempre encontrará el p-valor soñado. Hace bueno el refrán «El que busca, encuentra».