La región crítica en los contrastes de hipótesis
2025-11-03
La región crítica en los contrastes de hipótesis
Hace mucho, mucho tiempo, el contraste estadístico de hipótesis se fundamentaba en la región crítica. Con el advenimiento de la computación, el p-valor reinó en la Terra Scientia proveyendo felilicidad y bienestar a sus habitantes. La región crítica, considerada como la zona oscura y tenebrosa, quedó relegada y casi olvidada; solo los más ancianos del lugar recuerdan su existencia.
Pero ha llegado la hora de destronar al p-valor y recuperar la región crítica.

La definición de región crítica o de rechazo
La región crítica \(C\) a un nivel de significación \(\alpha\) representa el subconjunto del espacio muestral tal que la probabilidad de que la muestra aleatoria simple \((\xi_1,\xi_2,\ldots,\xi_n)\) pertenezca a \(C\), cuando \(H_0\) es cierta, es igual a \(\alpha\), es decir, \[Pr((\xi_1,\xi_2,\ldots,\xi_n) \in C \, | \, H_0) = \alpha.\]
Así, la regla de decisión en un test queda siempre definida de acuerdo a una región crítica, y no a que p-valor<0.05. Si la muestra obtenida en el experimento se ubica dentro de la región crítica, rechazamos la hipótesis nula. En caso de que no se encuentre dentro de dicha región, no rechazamos la hipótesis nula.
Por definición, la probabilidad de obtener resultados que conduzcan al rechazo de la hipótesis nula es \( \alpha\), suponiendo que ésta sea la verdadera. De entre las posibles regiones críticas que cumplen esta condición, escogemos la que minimice el error de tipo II (mayor potencia).
La región de no-rechazo constituye el complementario de la región crítica. Su probabilidad se denomina nivel de confianza y se representa por \(1- \alpha\). El valor crítico \(C_{0}\) divide a ambas regiones (la crítica y la de no-rechazo).
Como la información contenida en la muestra se resume en un estadístico \(T\), resulta conveniente caracterizar la región crítica en función del estadístico empleado. Y por consiguiente, conocer la distribución probabilística de \(T\) resulta fundamental para calcular las probabilidades asociadas.
Nivel de significación \( \alpha\). Probabilidad de error tipo I
De entre el conjunto de expedientes depositados en una oficina, examinamos diez expedientes para revisar si llevan la firma de autorización correspondiente. Supongamos que son independientes e idénticamente distribuidos. Deseamos contrastar que al menos el 90% de la documentación de la oficina se conforma correctamente. En caso de encontrar siete o menos expedientes correctos, rechazamos la hipótesis nula.
La hipótesis nula en este caso es \(H_{0}: p \ge 0.9\) versus la hipótesis alternativa \(H_{1}: p < 0.9\), con \(p\) la proporción real de documentos correctos en la oficina. La región crítica, que nos lleva a rechazar la hipótesis nula, es \[C=\{0,1,2,3,4,5,6,7\}.\] Si al examinar los diez documentos encontramos menos de ocho conformados, rechazamos la hipótesis nula y concluimos que el porcentaje de documentación correcta es menor del 90%, (\(H_{1}: p < 0.9\)).
Representemos por \(X\) el número de documentos correctos en una muestra de diez documentos. Si suponemos la hipótesis nula cierta, entonces la probabilidad de éxito en cada intento es \(p=0.9\). Hemos seleccionado la situación más desfavorable de \(H_{0}\), que ocurre cuando \(p=0.9\): \[Pr(X \in \{0,1,2,3,4,5,6,7\} \, | \, H_{0})= Pr(X \in \{0,1,2,3,4,5,6,7\} \, | \, p\ge 0.9) \le Pr(X \in \{0,1,2,3,4,5,6,7\} \, | \, p= 0.9).\]
El cálculo de probabilidades señala que \(X \sim Binom(n=10,p=0.9)\), por lo que la probabilidad asociada a la región crítica es
pbinom(7, size = 10, prob = 0.9) # Pr(Binom(10,0.9) <= 7)
[1] 0.07019083
que representa el nivel de significación de nuestro test, \(\alpha=0.07\).
O de forma equivalente, con esta regla de decisión (rechazar \(H_{0}\) si encontramos siete o menos expedientes correctos) existe un siete por ciento de rechazar la hipótesis nula cuando ésta es correcta y cometer el denominado error de tipo I.
Probabilidad de error tipo II \( \beta\). Potencia
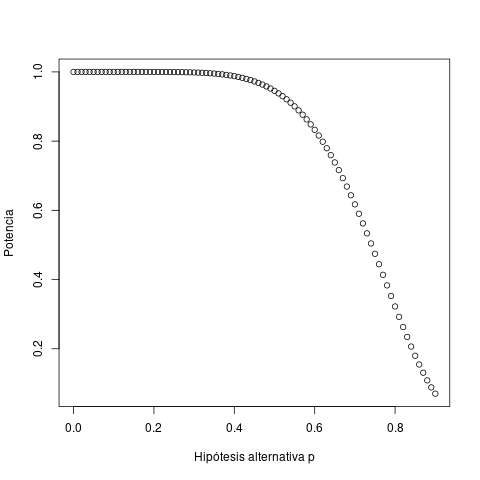
El error de tipo II consiste en no seleccionar la hipótesis alternativa cuando ésta es la verdadera. \( \beta\) representa la probabilidad de cometer este error y la potencia, definida como \(1- \beta\), la probabilidad de rechazar la hipótesis nula cuando resulta falsa. \[ \beta=Pr(X \not\in C \, | \, H_{1}) = Pr(X\in\{8, 9, 10\}\, | \, p < 0.9)\] La función de potencia de un contraste depende de la hipótesis alternativa. Así, en este ejemplo \(Pot(p) = 1-Pr(X \in \{ 8,9,10 \} \, | \, p)\), con \(0 \le p <0.9\), y aplicando que \(X\) sigue una distribución binomial, \(Pot(p) = \sum_{k=0}^{7} Pr(Binomial(10,p)=k)\).
p <- c(0:90)/100 plot(p, pbinom(7,10,p), ylab="Potencia",xlab="Hipótesis alternativa p" )
Una introducción a los contrastes de hipótesis
Esta entrada forma parte de un serie de artículos introductorios sobre contrastes de hipótesis: